sataniC++

C++、競プロ、数学などについて色々考えたりします。

繰り返し自乗法

アルゴリズム アルゴリズム-か

概要

N^P \pmod{M}の値を効率的に解きます。


使える状況

「N^PをMで割ったあまり」が欲しいときに、Pがあまりにも大きいとその計算だけで時間がかかってしまうことがあります。そのような時には、この繰り返し自乗法を用いることで素早く求めることが出来ます。


説明

N^P \pmod{M}の値を求めたいとき、愚直な方法として次のような手法を考えることが出来ます。

using ll = long long int;
ll PowMod(ll N, ll P, ll M){
    ll ans = 1;
    for(ll i=0; i<P; ++i){
        ans *= N;
        ans %= M;
    }
    return ans;
}

しかし、上記のような方法だとP回ループしてしまうため、P=10^9などの場合では非常に時間がかかってしまいます。


そこで使うのが、繰り返し自乗法です。


繰り返し自乗法は、

「Nを一回一回掛けてmodを取るのでは時間がかかるので、まとめて掛けてしまおう！」

という考えをもとにしたアルゴリズムです。


この「まとめて掛ける」というのがどういうことか、具体的にP=20のときについて考えながら説明します。


以下、求める値をX、N^{(i)}:=N^i \pmod{M}とし、また、"\times"の計算をした時にはMで割った余りを求める操作も一緒に行っているものとします。

ボトムアップ(小さい値から大きい値へと計算していく)な考え方

先ほどの愚直な方法では、次のような計算をしていることになります。
\displaystyle \begin{eqnarray} X &=& N^{(1)}\times N^{(1)}\times N^{(1)}\times N^{(1)}\times N^{(1)}\times \cdots \times N^{(1)}\\ &=& N^{(2)}\times N^{(1)}\times N^{(1)}\times N^{(1)}\times \cdots \times N^{(1)}\\ &=& N^{(3)}\times N^{(1)}\times N^{(1)}\times \cdots \times N^{(1)}\\ &&\vdots\\ &=& N^{(19)}\times N^{(1)}\\ &=& N^{(20)} \end{eqnarray}
確かに、P回、つまり20回分の計算をしていることがわかりますね。


ここで、上で計算しているように、
N^{(2)} = N^{(1)}\times N^{(1)}
となっていることから、
\displaystyle \begin{eqnarray} X &=& N^{(1)}\times N^{(1)}\times N^{(1)}\times N^{(1)}\times \cdots \times N^{(1)}\times N^{(1)}\\ &=& (N^{(1)}\times N^{(1)})\times (N^{(1)}\times N^{(1)})\times \cdots \times (N^{(1)}\times N^{(1)})\\ &=& N^{(2)}\times N^{(2)}\times \cdots \times N^{(2)}\\ \end{eqnarray}

とまとめてしまい、あとは、
\displaystyle \begin{eqnarray} X &=& N^{(2)}\times N^{(2)}\times N^{(2)}\times N^{(2)}\times \cdots \times N^{(2)}\\ &=& N^{(4)}\times N^{(2)}\times N^{(2)}\times \cdots \times N^{(2)}\\ &=& N^{(6)}\times N^{(2)}\times \cdots \times N^{(2)}\\ &&\vdots\\ &=& N^{(18)}\times N^{(2)}\\ &=& N^{(20)} \end{eqnarray}

と出来るので、計算回数は最初のN^{(2)}を計算する1回と、まとめた後の10回となっているので、見事に半分にすることが出来ていますね。

これをさらに、
N^{(4)}=N^{(2)}\times N^{(2)}
とすることによりN^{(4)}を求め、同様にN^{(8)}を求め、…と繰り返すことで、最終的には
\displaystyle \begin{eqnarray} X &=& N^{(16)} \times N^{(4)}\\ &=& N^{(20)} \end{eqnarray}

とまで式を短くすることが出来ます。
このとき、次の5回しか計算をしていないことが分かりますね。

  1. N^{(2)}を求める(N^{(1)}\times N^{(1)})
  2. N^{(4)}を求める(N^{(2)}\times N^{(2)})
  3. N^{(8)}を求める(N^{(4)}\times N^{(4)})
  4. N^{(16)}を求める(N^{(8)}\times N^{(8)})
  5. N^{(20)}を求める(N^{(16)}\times N^{(4)})


このように、Nの自乗を繰り返し計算した結果を用いて計算を行っているので、「繰り返し自乗法」と言うんですね。

トップダウン(大きい値から小さい値へと計算していく)な考え方

先ほどの方法とほとんど変わりませんが、実装が(少しだけ)簡単な方法もあります。
おそらく、一般的に「繰り返し自乗法」と言ったときにはこちらの方を指すのではないでしょうか。


この方法は、次のように再帰的な式で書き表すことが出来ます。
\displaystyle N^P = \left\{ \begin{array}{ll} 1 & (P=0)\\ \left(N^{P/2}\right)^2 & (P:偶数)\\ N \times N^{P-1} & (P:奇数) \end{array} \right.


この式を用いて、先ほどのP=20の時についてを計算してみましょう。
\displaystyle \begin{eqnarray} N^{(20)} &=& \left(N^{(10)}\right)^2\\ &=& \left(\left(N^{(5)}\right)^2\right)^2\\ &=& \left(\left(N^{(1)}\times N^{(4)}\right)^2\right)^2\\ &=& \left(\left(N^{(1)}\times \left(N^{(2)}\right)^2\right)^2\right)^2\\ &=& \left(\left(N^{(1)}\times \left(\left(N^{(1)}\right)^2\right)^2\right)^2\right)^2\\ \end{eqnarray}

よって、先ほどと同様に5回の計算でN^{(20)}を求めることが出来ています。


コード(C++)

using ll = long long int;
ll RepeatSquaring(ll N, ll P, ll M){
    if(P==0) return 1;
    if(P%2==0){
        ll t = RepeatSquaring(N, P/2, M);
        return t*t % M;
    }
    return N * RepeatSquaring(N, P-1, M);
}

コードの説明

トップダウンな考え方の節で示した式を、そのまま関数に落とし込んでいるだけです。


具体例

2^{1000000000} \pmod{1000000007}の値を求める。

今回は、愚直な方法(関数PowMod_Simple)と繰り返し自乗法(PowMod_RepeatSquaring)でどのくらい性能の差があるかを、

  • 再帰回数(再帰orループするたびにカウント)
  • 処理時間(std::chronoを用いて計測)

の2点について見てみます。

#include <iostream>
#include <algorithm>
#include <chrono>

using ll = long long int;

ll count_ps = 0;
ll PowMod_Simple(ll N, ll P, ll M){
    ll ans = 1;
    for(ll i=0; i<P; ++i){
        ++count_ps;
        ans *= N;
        ans %= M;
    }
    return ans;
}

ll count_prs = 0;
ll PowMod_RepeatSquaring(ll N, ll P, ll M){
    ++count_prs;
    if(P==0) return 1;
    if(P%2==0){
        ll t = PowMod_RepeatSquaring(N, P/2, M);
        return t*t % M;
    }
    return N * PowMod_RepeatSquaring(N, P-1, M);
}

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    
    //愚直な方法-----------------------------
    std::cout << "愚直な方法\n";
    auto startTime = std::chrono::system_clock::now();
    //処理部------
    std::cout << "2^1000000000 mod 1000000007 = " << PowMod_Simple(2, 1000000000, 1000000007) << "\n";
    std::cout << "再帰回数\t:" << count_ps << "\n";
    //------------
    auto endTime = std::chrono::system_clock::now();
    std::cout << "処理時間:" << std::chrono::duration_cast<std::chrono::nanoseconds>(endTime - startTime).count() << "ns\n";
    //---------------------------------------
    
    std::cout << "------\n";
    
    //愚直な方法-----------------------------
    std::cout << "繰り返し自乗法\n";
    startTime = std::chrono::system_clock::now();
    //処理部------
    std::cout << "2^1000000000 mod 1000000007 = " << PowMod_RepeatSquaring(2, 1000000000, 1000000007) << "\n";
    std::cout << "再帰回数\t:" << count_prs << "\n";
    //------------
    endTime = std::chrono::system_clock::now();
    std::cout << "処理時間:" << std::chrono::duration_cast<std::chrono::nanoseconds>(endTime - startTime).count() << "ns\n";
    //---------------------------------------
    
    return 0;
}
実行結果(一例)
愚直な方法
2^1000000000 mod 1000000007 = 140625001
再帰回数	:1000000000
処理時間	:22322817871ns
------
繰り返し自乗法
2^1000000000 mod 1000000007 = 140625001
再帰回数	:43
処理時間	:2709ns

この結果からも分かるように、再帰回数、処理時間ともに、文字通り桁違いで小さく計算することが出来ていますね。
ちなみに、処理時間の「ns」は「ナノ秒(ナノ=10^{-9})」を表しているため、

  • 愚直な方法 :22.322817871秒
  • 繰り返し自乗法 : 0.000002709秒

の時間がかかっていることを表しています。


備考

愚直な方法は計算量がO(P)であるのに対し、繰り返し自乗法ではO(\log P)にまで抑えられています。


あとがき

繰り返し自乗法は使いどころ(累乗の割った余りを求めたいとき)が分かりやすく、また実装も軽めなので、習得しやすいアルゴリズムだと思います。
一度この関連の問題を解いたら、また同じ場面に出会ったときに「あの再帰のやつだ…！」と思い出すことが出来ると思うので、ATC002Bなどで経験しておくと良いでしょう。

SRM688(Div2)に参加しました！

競プロ参加 競プロ参加-SRM

競プロのカレンダーを見ていると、2016/04/16 00:00(日本時間)からSRMがあるということだったので、TopCoder SRMに初参戦してみました。


初参戦ということでレートは1200から始まり、Div2の問題を解くみたいですね。


さっそくスタート！

Coding Phase

Easy(250)

「括弧の深さ…これどっかでやったことあるな…」と思い、迷わずいもす法で解くことを決めました。

#include <algorithm>
#include <string>
#include <vector>
 
class ParenthesesDiv2Easy {
    public:
    int getDepth(std::string s){
        int n = s.size();
        std::vector<int> depth(n, 0);
        std::vector<int> cumSum(n, 0);
        for(int i=0; i<n; ++i){
            if(s[i]=='('){
                ++depth[i];
            }else{
                --depth[i];
            }
        }
        cumSum[0]=depth[0];
        for(int i=1; i<n; ++i){
            cumSum[i]=cumSum[i-1]+depth[i];
        }
        std::sort(cumSum.begin(), cumSum.end());
        return cumSum[n-1];
    }
};

サンプルケースも結構すんなり通ったので、これで提出。
これにはあまり時間がかかりませんでした。

Medium(500)

「深さがマイナスになってたり最後の深さが0になってなかったりしたらおかしいよな…」
みたいなことをベースに色々やりました。

確か「)」を「(」にしたらそれ以降の深さがすべて+2されて、
逆に「(」を「)」にしたらそれ以降の深さがすべて-2される、
ということを基本に考えて以下のように書いてみました。

#include <algorithm>
#include <string>
#include <vector>
 
class ParenthesesDiv2Medium {
    public:
    std::vector<int> correct(std::string s){
        int n = s.size();
        std::vector<int> depth(n, 0);
        std::vector<int> cumSum(n, 0);
        for(int i=0; i<n; ++i){
            if(s[i]=='('){
                ++depth[i];
            }else{
                --depth[i];
            }
        }
        cumSum[0]=depth[0];
        for(int i=1; i<n; ++i){
            cumSum[i]=cumSum[i-1]+depth[i];
        }
        std::vector<int> ans;
        for(int i=0; i<n; ++i){
            if(cumSum[i]<0){
                ans.push_back(i);
                for(int j=i; j<n; ++j){
                    cumSum[j]+=2;
                }
            }
        }
        if(cumSum[n-1]!=0){
            for(int i=n-2; i>=0; --i){
                if(cumSum[i]<2 && cumSum[i+1]>=2){
                    ans.push_back(i+1);
                    for(int j=i+1; j<n; ++j){
                        cumSum[j]-=2;
                    }
                    i=n;
                    if(cumSum[n-1]==0){
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

ちょいちょい調整しながらサンプルケースが全部通ったところで提出。
割と時間がかかってしまいましたが、そのままHardへと進んで行きました。

Hard(1000)

LとRで指定された範囲外の各括弧の数を記録しておいて…とかやった気がします(遠い目)。

何回やっても結局サンプルケースがすべて通ることなくタイムオーバー。
あとちょっと…なような気がしてましたがはたして本当にそうだったのかはわかりません。


Challenge Phase

(この前の5分休憩の時にトイレ行ってたらもうこのフェイズ始まってて焦ったのは秘密)

このChallenge PhaseというものがTopCoder特有(？)で、とても新鮮でしたね。
「他の人のコード見て判断って、こんなん本当に出来るのかな」とちょっと不安もありました。


ところが、
「あれ、なんでここで0代入してるんだ…。これ間違ってるんじゃないのか？」みたいなのを発見して、これはいきなりチャレンジ成功！？…とか思ってたんですが…

となってしまいました(白目)。
結局どうしたら良いのかもよく分からず…

自分の環境ではArenaがなんだか重かったので、もしかしたら表示バグでも起こしてたのかもしれませんね。


というわけで、次のSRMでの目標が早速出来てしまいました(笑)。
次のSRMは2016/04/24 01:00(日本時間)なので、そこでChallengeにリベンジしてみたいと思います。


最終結果

スコア
問題 満点スコア 獲得スコア かかった時間
Easy 250 236.15 06:57
Medium 500 284.99 29:55
Hard 1000 0.00 --:--

計:521.14

レート

1200(白)→1231(青)


あとがき

初めてのSRMでしたが、なんとなくやったことがあるような問題だったので割と健闘出来ました。
レートも上がって…ってこれ、1200以上になったってことは次Div1なのでは…？(冷汗)

…次のSRMも張り切って頑張りたいと思います。

yukicoder No.22 括弧の対応

yukicoder yukicoder-★

問題

問題のURLはこちらです。
No.22 括弧の対応 - yukicoder


考えたこと

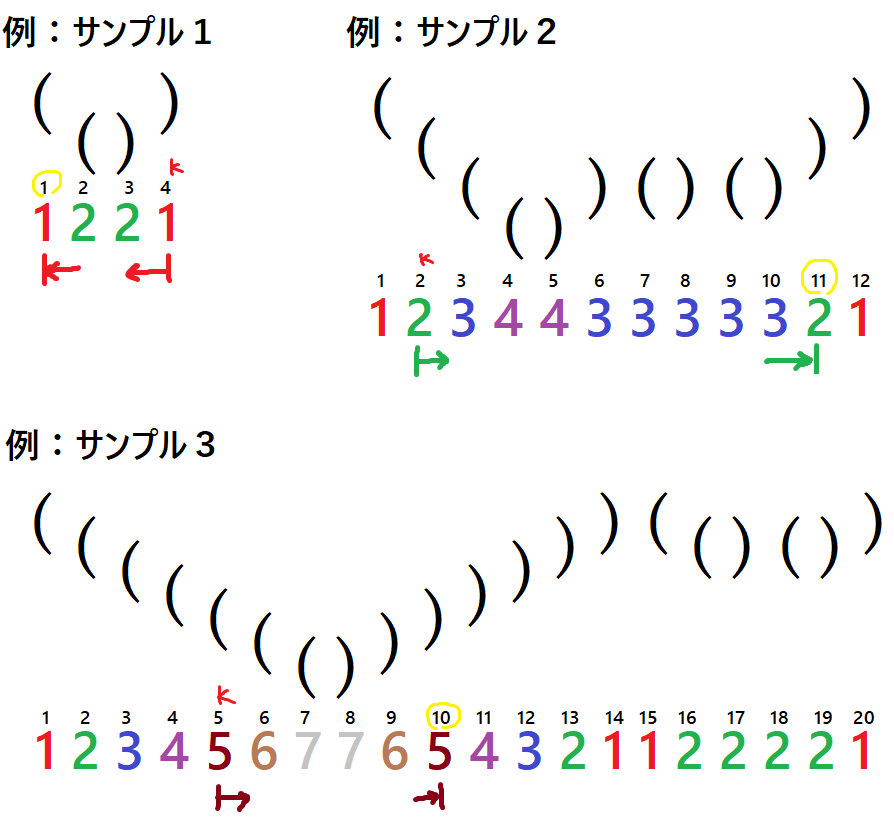
まず、入力された各括弧の深さを表す配列をいもす法を使って格納しておきます。

いもす法に関しては、こちらの記事を参照してください。
satanic0258.hatenablog.com

そして、調べるK番目の括弧が

  • 「(」なら、右方向へ
  • 「)」なら、左方向へ

K番目の括弧と同じ深さの括弧を探していきます。
それで一番最初に見つかったものが、K番目に対応する括弧となります。

f:id:satanic0258:20160409115525p:plain


コード(C++)

#86196 No.22 括弧の対応 - yukicoder

#include <iostream>
#include <vector>

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    char check;
    int N, K, ans;
    std::cin >> N >> K;
    std::vector<int> bracket(N+1, 0);
    for(int i=0; i<N; ++i){
        char input;
        std::cin >> input;
        if(i==K-1) check=input;
        switch(input){
            case '(': ++bracket[i]; break;
            case ')': --bracket[i+1]; break;
        }
    }
    for(int i=1; i<N+1; ++i){
        bracket[i] += bracket[i-1];
    }
    if(check=='('){
        ans=K+1;
        while(bracket[K-1]!=bracket[ans-1]) ++ans;
    }else{
        ans=K-1;
        while(bracket[K-1]!=bracket[ans-1]) --ans;
    }
    std::cout << ans << "\n";
            
    return 0;
}

コードの説明など

for(int i=0; i<N; ++i){
    char input;
    std::cin >> input;
    if(i==K-1) check=input;
    switch(input){
        case '(': ++bracket[i]; break;
        case ')': --bracket[i+1]; break;
    }
}
for(int i=1; i<N+1; ++i){
    bracket[i] += bracket[i-1];
}

この部分では、「いもす法」で各括弧の深さを配列bracketに入れています。

if(check=='('){
    ans=K+1;
    while(bracket[K-1]!=bracket[ans-1]) ++ans;
}else{
    ans=K-1;
    while(bracket[K-1]!=bracket[ans-1]) --ans;
}

この部分では、「考えたこと」でも述べたようにK番目の括弧に対応する括弧が何番目にあるかを調べています。


備考

この方法では、「各括弧の深さを求める（O(N)）」＋「K番目と同じ深さの括弧を探す（O(N)）」という２つの処理を行っています。

しかし、他の方の解説を見ると「K番目の深さを基準として一方向に移動しながら相対的な深さが0になるところを探す（O(N)）」や「初めから調べて開き括弧なら位置番号をstackに格納して、閉じ括弧ならstackの先頭要素を削除していき、どちらか一方がKであったとき、もう一方を答とする（O(N)）」など、この解説とは別の解答もあります。


よって、この記事の方法が唯一の解だということはありません。


感想など

やはり他の方の回答には、いくらか効率的であったり簡単であるものがあると思います。

そのため、「なんとか自力でAC出来た！」という時も、他の方の回答を見てみることで新たな発見があったり、勉強になることもあるので、問題を解いたらそのままにすること無く復習をしていくこともスキル上達のために必要なことではないでしょうか。


…と、自分の解法と他の方の解説との違いを改めて認識させられた問題だと思いました。