sataniC++

C++、競プロ、数学などについて色々考えたりします。

包除原理

数学 数学-集合

目標

ある複数の集合における和集合の要素の個数を共通部分に配慮して正しく計算する。


説明

以下、有限集合A,B,C,\cdotsは全て全体集合Uの中に真に含まれているもの、|A|はAの濃度（元の個数）とします。

2つの集合について

集合A,Bについて、「AまたはB（A\cup B）」であるものの集合の元の個数を求めてみましょう。
A\cup Bは、以下の図の赤い部分です。
f:id:satanic0258:20160410062119p:plain


まずは、「AまたはB」ということで単純に「Aの元の個数とBの元の個数の和」を見てみます（見やすさのために色を変えています）。
f:id:satanic0258:20160410070646p:plain

この図を見ると、以下の式が成り立っていることが分かりますね。
|A|+|B|=|A\cup B|+|A\cap B|

よって、以上の式を変形することで次のようにA\cup Bの元の個数を求めることが出来ました。
|A\cup B|=|A|+|B|-|A\cap B|


3つの集合について

次は、集合A,B,Cについて、「A\cup B\cup Cの元の個数」を求めてみましょう。

2つの集合のときと同様に、|A|+|B|+|C|を見てみます。
f:id:satanic0258:20160410080716p:plain


ここで、「AでありBであるがCではない」などの集合が最後に出てきていますが、こういった「○○でない」という集合（補集合と言います）は少し扱いにくいため、次のようなことをします。
f:id:satanic0258:20160410081326p:plain

こうすることで、補集合を用いずに以下の式が成り立つことが分かります。
|A|+|B|+|C|=|A\cup B\cup C|+|A\cap B|+|B\cap C|+|C\cap A|-|A\cap B\cap C|

よって、以上の式を変形することで次のように|A\cup B\cup C|を求めることが出来ました。
\displaystyle \begin{align} |A\cup B\cup C| &= |A|+|B|+|C|-(|A\cap B|+|B\cap C|+|C\cap A|-|A\cap B\cap C|)\\ &= |A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C| \end{align}


一般的な複数の集合について

ここでは詳しく触れませんが、n個の集合A_1,A_2,\cdotsにおける和集合\displaystyle \bigcup_i A_iの元の個数は、次のように表されます。

\displaystyle |\bigcup_i A_i|
\displaystyle = \sum_i |A_i|-\sum_{i < j} |A_i\cap A_j|+\sum_{i < j < k} |A_i\cap A_j\cap A_k|-\cdots +(-1)^{n-1}|A_1\cap \cdots A_n|


具体例

20以下の自然数のうち「3の倍数または5の倍数」であるものの個数を求める

今、全体集合U、集合A,Bを次のように定義します。
U:=\{20以下の自然数\}
A:=\{3の倍数\}=\{3,6,9,12,15,18\}
B:=\{5の倍数\}=\{5,10,15,20\}

また、このとき次のことがわかります。
A\cup B=\{3の倍数または5の倍数\}
A\cap B=\{3の倍数かつ5の倍数\}=\{15の倍数\}=\{15\}


よって、先ほどの式に代入すると、
\begin{align} |A\cup B|&=|A|+|B|-|A\cap B|\\ &=6+4-1\\ &=9 \end{align}

ゆえに、20以下の自然数のうち「3の倍数または5の倍数」であるものは9個あることがわかりました。

f:id:satanic0258:20160410100739p:plain


あとがき

今回は、図で説明したほうがわかりやすいと思ったので、図を多めにしてみました。
なお、上記ではA\cap B=\emptysetである場合については触れていませんが、同様に計算することが出来ます。
あらゆる場面において同じ式が適応出来るので、ひとたび上記の式を覚えることでどんな集合の個数に関する計算でも出来てしまいますね。

ちなみに、4つ以上の集合に関するベン図を書こうとしたとき、全て真円で書くことが出来ないことが証明されているらしいです。
別の方法として、4つの楕円を重ねる方法や、3つの真円に1つの湾曲した楕円を上手く重ねる方法などがあるらしいですが、実用的ではないようです。

yukicoder No.21 平均の差

yukicoder yukicoder-★

問題

問題のURLはこちらです。
No.21 平均の差 - yukicoder


考えたこと

グループの数Kは3以上であるため、「最大値と最小値の差」を求めれば良いですね。
グループの分け方としては、「最大値」「最小値」「余り」とします。

以下の図を見たら明らかですね。
（図中の赤い線は「入力n_i」、青い囲みは「グループ」、緑の点は「グループの平均値」を表しています）
f:id:satanic0258:20160406201308p:plain

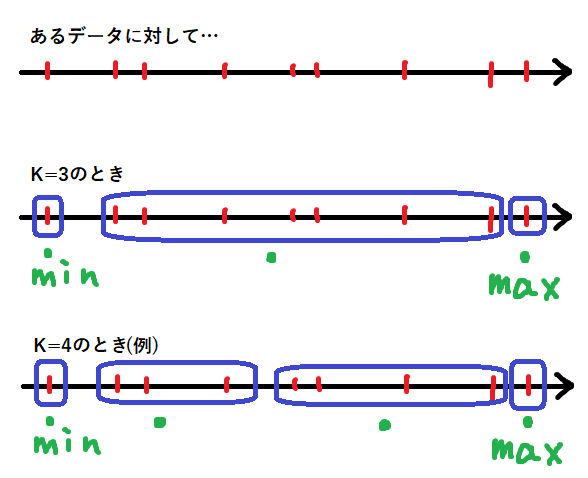
最大値と最小値のみを使っているので、余りはどのようなグループ分けをしてもいいことがわかりますね。

また、このことから入力Kは使うことはありません。


コード(C++)

#85889 No.21 平均の差 - yukicoder

#include <iostream>
#include <algorithm>

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    
    int N, K, maxNum=1, minNum=1000;
    std::cin >> N >> K;
    for(int i=0; i<N; ++i){
        int input;
        std::cin >> input;
        maxNum = std::max(maxNum, input);
        minNum = std::min(minNum, input);
    }
    std::cout << maxNum-minNum << "\n";

    return 0;
}

コードの説明など

入力されたデータ全てに対して、std::maxやstd::minで最大値maxNumや最小値minNumを更新しているだけです。

なお、maxNumとminNumの初期値ですが、「最大値はデータが取りうる最小の値」、「最小値はデータが取りうる最大の値」としています。これによって最初のデータからどんどん最大値・最小値を更新していくことが出来ます。


備考

一度だけデータの数のループを回しているので、計算量はO(N)で済みます。


感想など

ぱっと問題を見ると「平均値だからグループの分け方による各平均値の値を求めて…」となりそうですが、よく考えてみると最大と最小の値しか使わないことがわかります。

しかし問題文では「小数点以下を切り上げ…」とあったり、サンプルでは最小値だけを使わなくても求める値が出ていたりと、問題の作者さんの工夫が見られます。

このような発想の転換をすると効率的に解くことが出来る問題というのも競プロの問題には結構多いと思うので、頭をやわらかくして考えることが大事です。
簡単なケースなどで考えてみたり、紙に書いてみたりするといいんじゃないでしょうか。

yukicoder No.18 うーさー暗号

yukicoder yukicoder-★

問題

問題のURLはこちらです。
No.18 うーさー暗号 - yukicoder


考えたこと

i個目の文字について、

  1. 文字を数値に変換する
  2. その数値からi引く
  3. 数値を文字に変換する

と行えばよさそうですね。


コード(C++)

#85751 No.18 うーさー暗号 - yukicoder

#include <iostream>
#include <string>

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    
    std::string S;
    std::cin >> S;
    for(size_t i=0; i<S.size(); ++i){
        S[i] = ((S[i]-'A')-(i+1)+1300)%26+'A';
    }
    std::cout << S << "\n";

    return 0;
}

コードの説明など

入力に対して計算を行っているのはforループの中の1文のみなので、その右辺について順を追って説明します。

S[i]-'A'

ここでは「文字を数値に変換」しています。
C++では、半角アルファベットを数値（ASCIIコード）として扱っています。
その対応表は次のとおりです。

アルファベット A B C D ... X Y Z
ASCIIコード 0x41 0x42 0x43 0x44 ... 0x58 0x59 0x5A

（0x41は「16進数の41」を表します）

よって、「このアルファベットはAから数えて何番目なのか？」ということを調べたいときは、そのアルファベットから'A'（つまり0x41）だけ引いてやればいいのです。

S[i]の意味する文字 A B C D ... X Y Z
S[i]の数値（16進法表記） 0x41 0x42 0x43 0x44 ... 0x58 0x59 0x5A
S[i]の数値（10進法表記） 65 66 67 68 ... 88 89 90
S[i]-'A'（10進法表記） 0 1 2 3 ... 23 24 25

確かに、S[i]-'A'を計算することで、Aから数えて何番目かということがわかりますね。

(S[i]-'A')-(i+1)

次に、「数値からi引」いています。
コードではi+1引いていますが、配列の中身にアクセスする添字は0から始まるためです。

S[i]のi 0 1 2 3 ...
数えるとき 1文字目 2文字目 3文字目 4文字目 ...

と、添字のiとはちょうど1だけ大きいことがわかりますね。

((S[i]-'A')-(i+1)+1300)%26

ここでは、「Zの次はA」とループすることの計算をしています。

理想としては、計算した数値に対しするアルファベットは次のようになったらいいですね。

数値 0 1 2 ... 24 25 26 27 ... 50 51 52 53 ...
アルファベット A B C ... Y Z A B ... Y Z A B ...


では、どうしたら良いかというと、数値を26で割った余りを求めれば良いのです。
26で割った余りを欄を上の表に追加してみると、

数値 0 1 2 ... 24 25 26 27 ... 50 51 52 53 ...
数値を26で割った余り 0 1 2 ... 24 25 0 1 ... 24 25 0 1 ...
アルファベット A B C ... Y Z A B ... Y Z A B ...

となることがわかります（26はアルファベットA～Zまでの文字数です）。


ところで、C++での剰余（%）は「絶対値を割った余り」を算出してしまうようです。
具体的には次のような感じです。

ある整数Nに対して、

N ... -5 -4 -3 -2 -1 0 1 2 3 4 5 ...
N\% 3 ... -2 -1 0 -2 -1 0 1 2 0 1 2 ...


上記のコードで「(S[i]-'A')-(i+1)」としているため、入力文字数が最大である1024ほど大きいときには割られる数が負になることもあるのです。
これでは、最後に数値から文字に直す際におかしな事になってしまいますね。

その解決法として、割る数26の倍数であり1024より大きい1300を加える事で、入力がどんなものであったとしても必ず割られる数は正になるため、正確な「26で割った余り」を求めることが出来ます。

((S[i]-'A')-(i+1)+1300)%26+'A'

最後に、'A'を加える事によって「数値を文字に変換」することが出来ます。


あとはこれを各文字に対してループすると良いですね。


備考

計算量は、文字数に対するループのみなのでO(Sの文字数)ですね。


なお、C++のstd::stringでは、operator[](int)で参照・代入するときはchar型に変換されるので、Cと同じようなコードを書くことが出来ます。


感想など

この問題の「最後の次は最初に戻す」というような操作は、色々な場面で使えるものだと思います。
（ゲームでのカーソルの移動とか、ルーレットとかを想像したらわかりやすいですかね）

また、char型の文字に対する数値的な演算というものも覚えておいて損はないと思います。
この問題の「'A'を引いてAから何番目の文字かを調べる」といったことや、「'A'-'a'の値を使って大文字・小文字の変換をする」などが出来るので、あるとたまに役に立ったりします。


そのため、この問題を解くことで文字処理などの基本的なことの勉強になりますね。プログラミングを勉強し始めて少し経った頃に演習問題としてこの問題を解くと良いんじゃないでしょうか。